using the modes of the major scale to understand music theory
Music theory is essentially a communication tool. It's how musicians can describe sounds and common patterns in music. One of the first steps to understanding the theory is by learning what a mode is. Like a scale, a mode is simply a series of notes.
Relative Scales & Modes
Understanding the major scale and its modes will allow you to invoke different "colors" or feelings that the modes have to offer. The most basic way to understand what a mode is, is by seeing them relative to the scale they are based off of. For example, you could say the A Minor and C Major scales are two sides of the same coin.
C Major Scale
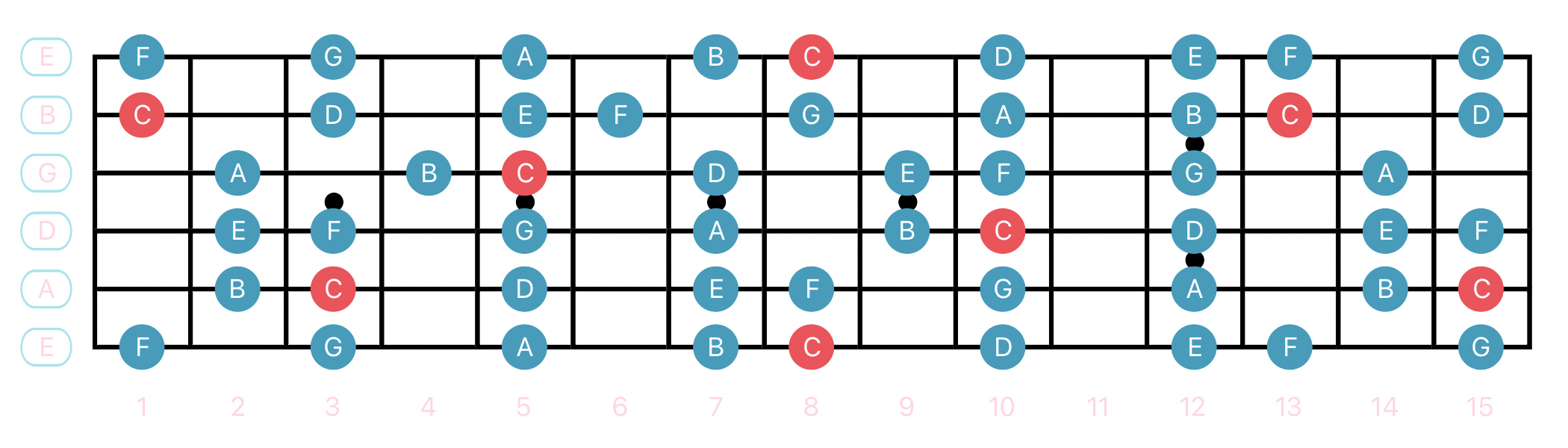
Let's also look at the chords built on top of the scale degrees.
| C | D | E | F | G | A | B |
|---|---|---|---|---|---|---|
C maj | D min | E min | F maj | G maj | A min | B dim |
A Minor Scale
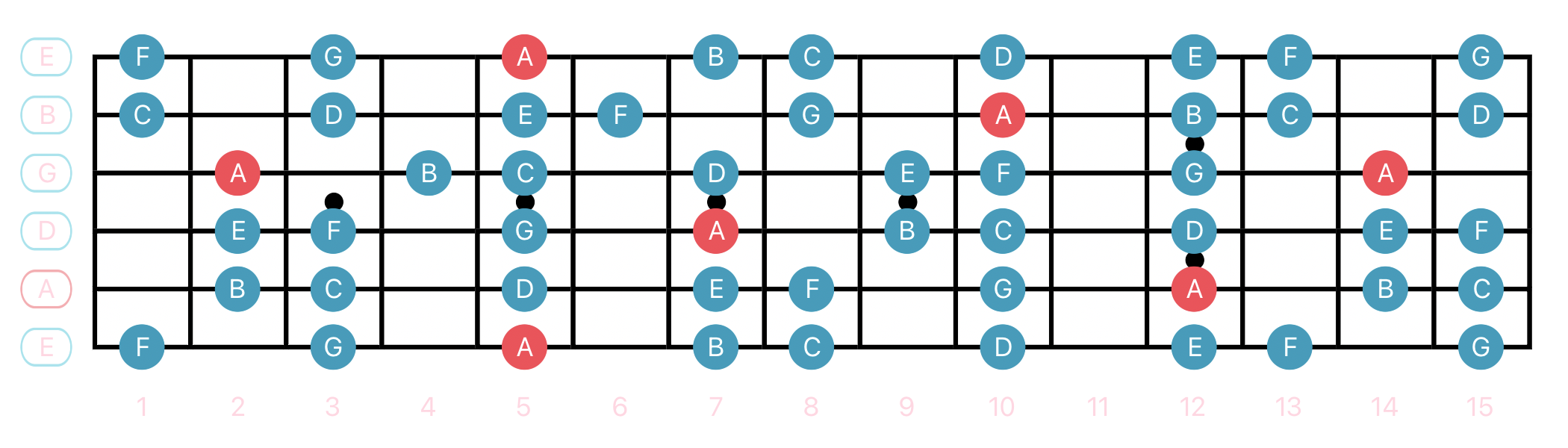
| A | B | C | D | E | F | G |
|---|---|---|---|---|---|---|
A min | B dim | C maj | D min | E min | F maj | G maj |
These are relative scales, implying that they have the same notes, but different starting points. A Minor is a mode of the C Major Scale, the 6th mode, and can be referred to as Aeolian or Natural Minor. They both share the same notes, C D E F G A B, but one starts at C and the other at A.
Since the major scale has 7 notes, it has 7 different modes, each with its own characteristic sound. For example, Dorian has a natural (♮) 6, and is the only one of the modes to have both a ♭3 and ♮6. If you're unfamiliar with terminology like this, keep reading for a review of these concepts down below. What you can take away from the Dorian mode right now, is that it creates the i min to iv maj chord progression, a unique and very popular sound (think Evil Ways - Santana). It's known to be a minor scale that is not exactly as dark as natural, due to having that iv maj chord instead of a iv min.
Don't worry if you're unfamiliar with the roman numeral system either, those are used instead of regular numbers to indicate they are chords. The concept to understand here is that the 4th scale degree would normally have a iv min built on top of it, but in Dorian we get a major chord.
Chords of D Dorian
| D | E | F | G | A | B | C |
|---|---|---|---|---|---|---|
D min | E min | F maj | G maj | A min | B dim | C maj |
Let's take a look at all of the scale degrees for each mode.
| Mode | Degrees | Color |
|---|---|---|
| Ionian | 1 2 3 4 5 6 7 | |
| Dorian | 1 2 ♭3 4 5 6 ♭7 | 6 |
| Phrygian | 1 ♭2 ♭3 4 5 ♭6 ♭7 | ♭2 |
| Lydian | 1 2 3 ♯4 5 6 7 | ♯4 |
| Mixolydian | 1 2 3 4 5 6 ♭7 | ♭7 |
| Aeolian | 1 2 ♭3 4 5 ♭6 ♭7 | ♭6 |
| Locrian | 1 ♭2 ♭3 4 ♭5 ♭6 ♭7 | ♭5 |
I didn't include a characteristic note for Ionian because it is our reference point, but you could say its characteristic notes are (♮) 4 and (♮) 7, being the only mode that has that pairing. If you're unfamiliar with the ♮, ♭ and ♯ symbols, they are known as accidentals.
♮ = natural ♭ = flat ♯ = sharp
What are scales?
Let's do a quick review of equal temperament, our musical system that divides the octave into 12 parts, or half steps, giving us the notes:
- C
- C♯/D♭
- D
- D♯/E♭
- E
- F
- F♯/G♭
- G
- G♯/A♭
- A
- A♯/B♭
- B
And then we loop back to C.
Half Steps & Whole Steps Take note how E & F and B & C are only a half step apart, while the other letters such as C to D are a whole step apart (a whole step is two half steps). If you're new to music in general, you might be wondering - what are these half steps and whole steps? A half step is the distance of one note, like moving from C to C♯/D♭, or E to F. A whole step is the distance of two notes. It would be like moving from C to D, or E to F♯/G♭.
Building Scales We use these half and whole steps to construct scales. In other words, different scales are different permutations of half steps and whole steps. The major scale half step & whole step pattern is below, made up of 2 whole steps, a half step, 3 whole steps, and then another half step before looping back around.
The Major Scale - whole step & half step pattern
flowchart TD subgraph Z[" "] direction LR classDef grey stroke:#17171f G[Whole Step]:::grey ~~~ A[Whole Step]:::grey A[Whole Step]:::grey ~~~ B[Half Step]:::grey end subgraph ZA[" "] direction LR C[Whole Step]:::grey ~~~ D[Whole Step]:::grey D[Whole Step]:::grey ~~~ E[Whole Step]:::grey E[Whole Step]:::grey ~~~ F[Half Step]:::grey end Z ~~~ ZA
We can visualize this by applying this pattern to some notes. Let's see it in C:
flowchart TD subgraph Z[" "] direction LR classDef highlight stroke:#fed7e2 classDef grey stroke:#17171f W[C]:::highlight ~~~ G[C#]:::grey G[C#]:::grey ~~~ I((D)):::highlight I[D]:::highlight ~~~ A[D#]:::grey A[D#]:::grey ~~~ O[E]:::highlight O[E]:::highlight ~~~ B[F]:::highlight end subgraph ZA[" "] direction LR Y[F#]:::grey ~~~ U[G]:::highlight U[G]:::highlight ~~~ D[G#]:::grey D[G#]:::grey ~~~ P[A]:::highlight P[A]:::highlight ~~~ E[A#]:::grey E[A#]:::grey ~~~ L[B]:::highlight L[B]:::highlight ~~~ F[C]:::highlight end Z ~~~ ZA
If we were to take this pattern, and change it by switching the 2nd and 3rd steps like below:
flowchart TD subgraph Z[" "] direction LR classDef grey stroke:#17171f G[Whole Step]:::grey ~~~ A[Whole Step] A[Whole Step]<---> B[Half Step] end Z
We'd be creating a different scale, which would be using the pattern whole step, half step, whole step, whole step, whole step, another whole step and then a half step.
The Melodic Minor Scale - whole step & half step pattern
flowchart TD subgraph Z[" "] direction LR classDef grey stroke:#17171f G[Whole Step]:::grey ~~~ A[Half Step] A[Half Step] ~~~ B[Whole Step] end subgraph ZA[" "] direction LR C[Whole Step]:::grey ~~~ D[Whole Step]:::grey D[Whole Step]:::grey ~~~ E[Whole Step]:::grey E[Whole Step]:::grey ~~~ F[Half Step]:::grey end Z ~~~ ZA
Again, we can visualize this by applying the pattern with C as the root:
flowchart TD subgraph Z[" "] direction LR classDef highlight stroke:#fed7e2 classDef theme stroke:#3F3FFF classDef grey stroke:#17171f W[C]:::highlight ~~~ G[C#]:::grey G[C#]:::grey ~~~ I[D]:::highlight I[D]:::highlight ~~~ A[D#] A[D#] ~~~ O[E]:::grey O[E]:::grey ~~~ B[F]:::highlight end subgraph ZA[" "] direction LR Y[F#]:::grey ~~~ U[G]:::highlight U[G]:::highlight ~~~ D[G#]:::grey D[G#]:::grey ~~~ P[A]:::highlight P[A]:::highlight ~~~ E[A#]:::grey E[A#]:::grey ~~~ L[B]:::highlight L[B]:::highlight ~~~ F[C]:::highlight end Z ~~~ ZA
We end up switching our E for a D♯/E♭, creating the C Melodic Minor scale and giving us the following degrees/notes:
| Degrees | 1 | 2 | ♭3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|---|
| notes | C | D | E♭ | F | G | A | B |
Even though this looks pretty similar to our regular major scale, that flatted 3rd creates a major difference in its sound (the 3rd degree of the scale defines whether it's going to have a major or minor sound to it). The 4 whole steps in a row gives an eerie quality to the rest of it. Meldodic Minor is especially satisfying when played in ascending order (because it includes the natural 7th scale degree which wants to resolve to 1).
C Melodic Minor Scale
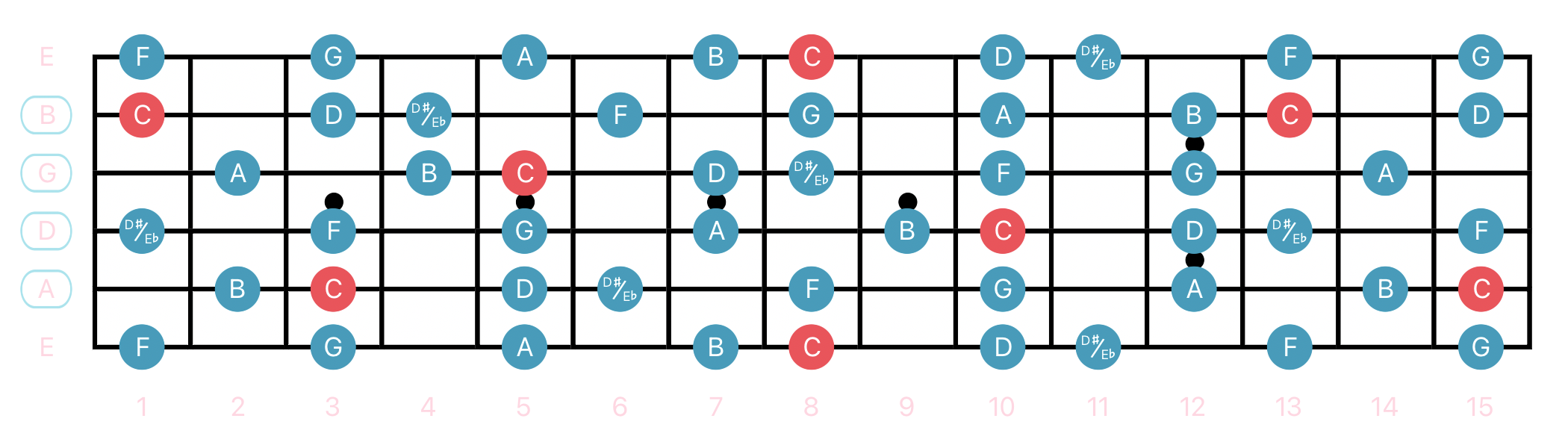
Melodic Minor is an acquired taste, but once your ears learn how to recognize it and you start finding ways to use it, it becomes addictive. Try it out!
Number System
Music theory is based on the major scale. We use it as a reference point to compare all other sounds. Most musical systems will do this (It's no coincidence that all the white keys on the piano make the C Major Scale). If you're not familiar with referring to scale degrees as abbreviated numbers relative to the 1, all you need to do is familiarize yourself with intervals.
Intervals are like chords - multiple notes played at the same time. But an interval is specifically two notes played at the same time - because of this, you can also think of an interval as the distance between those two notes.
| Interval | Abbreviated | In C | Half Steps |
|---|---|---|---|
| perfect unison | 1 | C | 0 |
| min 2nd | ♭2 | D♭ | 1 |
| maj 2nd | 2 | D | 2 |
| min 3rd | ♭3 | E♭ | 3 |
| maj 3rd | 3 | E | 4 |
| perfect 4th | 4 | F | 5 |
| diminished 5th | ♭5 | G♭ | 6 |
| perfect 5th | 5 | G | 7 |
| min 6th | ♭6 | A♭ | 8 |
| maj 6th | 6 | A | 9 |
| min 7th | ♭7 | B♭ | 10 |
| maj 7th | 7 | B | 11 |
| perfect octave | 8 | C | 12 |
Parallel Scales & Modes
I want to wrap up this part of the discussion with one more concept, which is understanding modes in parallel. Let's take another look at the Major and Natural Minor scales (Ionian and Aeolian modes), but this time we'll examine them in parallel.
C Major (Ionian)
| Degrees | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|---|
| notes | C | D | E | F | G | A | B |

C Natural Minor (Aeolian)
| Degrees | 1 | 2 | ♭3 | 4 | 5 | ♭6 | ♭7 |
|---|---|---|---|---|---|---|---|
| notes | C | D | E♭ | F | G | A♭ | B♭ |
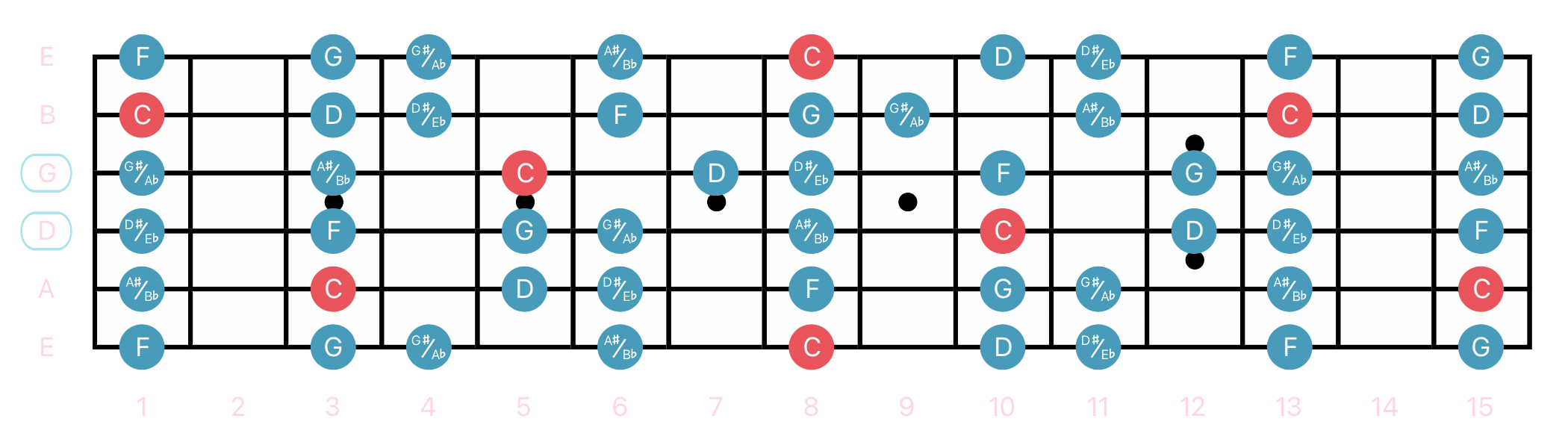
Two modes that are relative to each other share the same notes, but two modes that are parallel to each other share the same root. Looking at scales this way allows us to directly compare their scale degrees and hear the differences between them. As we can see above, the Aeolian mode has a ♭3, ♭6, and a ♭7.
How do we apply this to our practice regiment? Ideally, they should be memorized. Try reciting the two octave mode below, playing it in ascending order, and then back down.
Dorian Mode - 2 Octaves
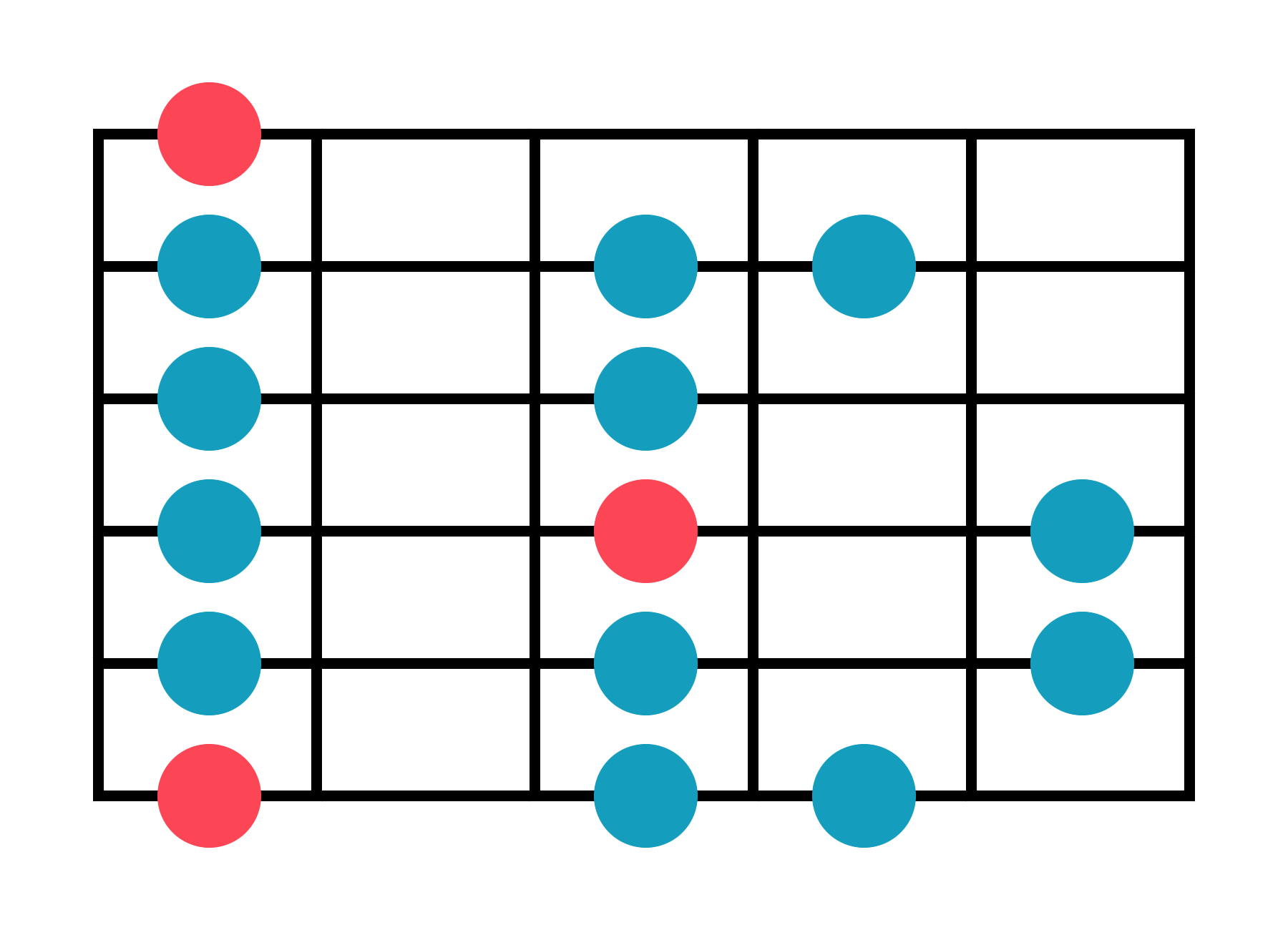
It helps to be familiar with how the mode fits into the general scale it's from. For the example below, in the key of D, you would take the Dorian Mode shape above and apply it to the 10th fret. You should be able to see how D Dorian is a relative mode of C Major/Ionian and shares the same notes, C D E F G A B, but starts from D (10th fret of the low E string).
D Dorian
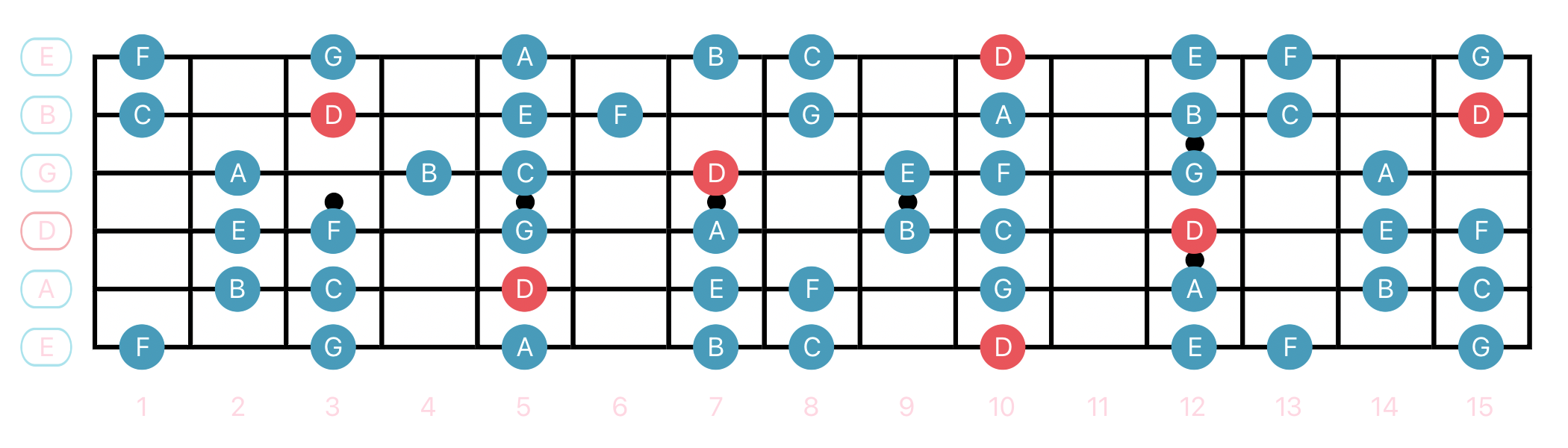
After becoming comfortable with all 7 of the modes from the major scale, the next step is applying this type of practice to the other 3 heptatonic scales, Melodic Minor, Harmonic Minor, and finally Harmonic Major. This means you have 28 Mode shapes to memorize. To get a deeper level of understanding, you can learn the diatonic chords of each mode as well, which means learning them as functions. Seeing the chords that are built upon each scale degree as numbers rather than notes helps us memorize the sound of the chord in relation to the center of the key we're in.
Chord Functions
Diatonic means to use only notes that are in the scale. Building diatonic chords on top of each of the C Major scale degrees gives us the following chords:
I maj | II min | III min | IV maj | V maj | VI min | VII dim |
|---|---|---|---|---|---|---|
C maj | D min | E min | F maj | G maj | A min | B dim |
Numbered analysis allows us to hear chords based on their relation to the tonic, the root of the key. Functions help us categorize chords based on their 'feeling'. The 3 types of functions are Tonic, Subdominant, and Dominant. We examine the function of chords to help us with reharmonization and other composition techniques. Reharmonization means to replace a chord with another, usually using the same function.
| Tonic | Subdominant | Dominant |
|---|---|---|
I maj | II min | V maj |
III min | IV maj | VII dim |
VI min |
Tonic refers to the root: the home. It is the term for conveying a sense of resolution. The first degree of any scale is actually called 'the Tonic'. It's used to denote the center of our key.
Chords in C Major
by function
| Tonic | Notes |
|---|---|
I maj | C - E - G |
III min | E - G - B |
VI min | A - C - E |
| Subdominant | Notes |
|---|---|
II min | D - F - A |
IV maj | F - A - C |
| Dominant | Notes |
|---|---|
V maj | G - B - D |
VII dim | B - D - F |
Dominant chords invoke dissonance, or simply put, the feeling of being away from home. A lot of music can be seen as a dance between tonic and dominant, moving back and forth. All the tonic chords contain the 3rd degree, also known as the mediant. In the key of C, the mediant is E. All the dominant chords contain a B, or the 7th degree of the scale, known as the leading tone.
flowchart TD subgraph Z[" "] classDef grey stroke:#17171f direction LR A[Dominant]:::grey ---> B[Tonic]:::grey end Z
The leading tone and the mediant both have very special jobs in the major scale. The leading tone is unstable, and the mediant is stable. All this means is that when we hear a B in the key C (the leading tone), our ear expects to hear a resolution. We expect to hear that B move to C. On the other side of the spectrum, when we hear an E (the mediant), we feel resolution, and can sit comfortably in that space.
Subdominant is a special function. It represents a place that isn't home, but not quite as dissonant as dominant function. Subdominant chords are generally used to create breaks in a phrase or to bring the song to a new place. The most evident uses of these functions can be found in the classic I, IV, V chord progression.
| Tonic | Subdominant | Dominant |
|---|---|---|
I | IV | V |
C | F | G |
Borrowing Chords in Compositions
Thank you for reading and I hope I've gotten you thinking more about the modes, music theory, chord functions, and how these concepts can work together to influence your compositions. Recognizing/knowing the sound of each mode can give us a wide array of places to bring our songs to. Thinking about the tonic/dominant nature of music can help you write transitions, reharmonize songs and in general improve your overall understanding of music. The real magic comes from combining these ideas - essentially borrowing chords from different modes, and using them either temporarily or invoking drastic changes by modulating to these new places.
Modulation vs Borrowing Chords One of the most popular places to borrow chords from is subdominant minor. We can infer what that means by examining chord functions for the minor scale. (Notice how we use lowercase roman numerals for minor scale analysis)
Minor Scale Analysis & Chord Functions
i min | ii dim | ♭iii maj | iv min | v min | ♭vi maj | ♭vii maj |
|---|---|---|---|---|---|---|
C min | D dim | E♭ maj | F min | G min | A♭ maj | B♭ maj |
| Tonic | Subdominant | Dominant |
|---|---|---|
i min | ii dim | v min |
♭iii maj | iv min | ♭vii maj |
♭vi maj |
We can do whatever we want in our music. The possibilities are seemingly endless. We use parallel scales to get ideas on what chords we can jump to, whether we're using the chord briefly (borrowing) or we want to take the entire song to a new place for a section, maybe a bridge or ending (modulation). This could also be referred to as modal interchange.
flowchart TD subgraph Z[" "] direction LR classDef grey stroke:#17171f G[F maj]:::grey ~~~ A[F min] A[F min] ~~~ B[C maj]:::grey end Z
A common example of modal interchange is borrowing the iv min chord from the minor scale. We're using the subdominant minor sound to bring a new emotion into play, and this F min allows us to introduce an A♭ into the melody.
| Chord | Notes |
|---|---|
I maj | C - E - G |
IV maj | F - A - C |
IV min | F - A♭ - C |
Summary
To end this post I'm going to post an index of the major scale modes and their chord functions below. I hope this paints a bigger picture , and helps others visually understand the modes. The most important thing is that you recite these scales & modes so your ears can learn them too.
Major Scale - Mode Degrees
| Ionian | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|---|
| Dorian | 1 | 2 | ♭3 | 4 | 5 | 6 | ♭7 |
| Phrygian | 1 | ♭2 | ♭3 | 4 | 5 | ♭6 | ♭7 |
| Lydian | 1 | 2 | 3 | ♯4 | 5 | 6 | 7 |
| Mixolydian | 1 | 2 | 3 | 4 | 5 | 6 | ♭7 |
| Aeolian | 1 | 2 | ♭3 | 4 | 5 | ♭6 | ♭7 |
| Locrian | 1 | ♭2 | ♭3 | 4 | ♭5 | ♭6 | ♭7 |
Major Scale - Mode Degrees in C
| Ionian | C | D | E | F | G | A | B |
|---|---|---|---|---|---|---|---|
| Dorian | C | D | E♭ | 4 | 5 | 6 | B♭ |
| Phrygian | C | D♭ | E♭ | 4 | 5 | A♭ | B♭ |
| Lydian | C | D | E | F♯ | 5 | 6 | 7 |
| Mixolydian | C | D | E | 4 | 5 | 6 | B♭ |
| Aeolian | C | D | E♭ | 4 | 5 | A♭ | B♭ |
| Locrian | C | D♭ | E♭ | 4 | G♭ | A♭ | B♭ |
Major Scale Modes - Chord Analysis
Diatonic Chords in C (parallel)
Ionian (Major Scale)
I maj | II min | III min | IV maj | V maj | VI min | VII dim |
|---|---|---|---|---|---|---|
C maj | D min | E min | F maj | G maj | A min | B dim |
Dorian
i min | ii min | ♭iii maj | iv maj | v min | vi dim | ♭vii maj |
|---|---|---|---|---|---|---|
C min | D min | E♭ maj | F maj | G min | A dim | B♭ maj |
Phrygian
i min | ♭ii maj | ♭iii maj | iv min | v dim | ♭vi maj | ♭vii min |
|---|---|---|---|---|---|---|
C min | D♭ maj | E♭ maj | F min | G dim | A♭ maj | B♭ min |
Lydian
I maj | II maj | III min | ♯IV dim | V maj | VI min | VII min |
|---|---|---|---|---|---|---|
C maj | D maj | E min | F♯ dim | G maj | A min | B min |
Mixolydian
I maj | II min | III dim | IV maj | V min | VI min | ♭VII maj |
|---|---|---|---|---|---|---|
C maj | D min | E dim | F maj | G min | A min | B♭ maj |
Aeolian (Minor Scale)
i min | ii dim | ♭iii maj | iv min | v min | ♭vi maj | ♭vii maj |
|---|---|---|---|---|---|---|
C min | D dim | E♭ maj | F min | G min | A♭ maj | B♭ maj |
Locrian
I dim | ♭II maj | ♭III min | IV min | ♭V maj | ♭VI maj | ♭VII min |
|---|---|---|---|---|---|---|
C dim | D♭ maj | E♭ min | F min | G♭ maj | A♭ maj | B♭ min |
Major Scale - Guitar Mode Practice Forms
(with their counterpart scales relative to C)
Ionian - Two Octaves
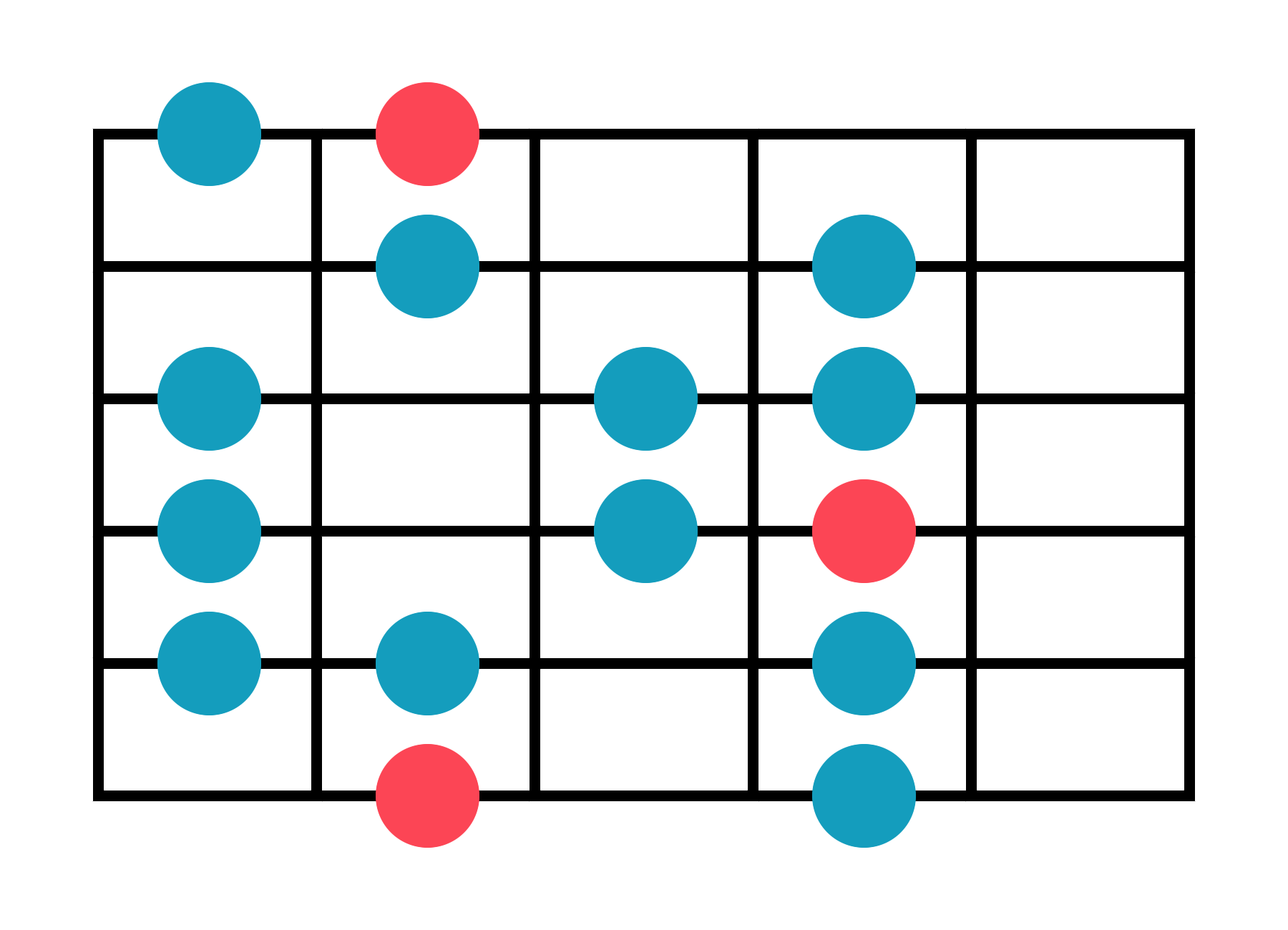
C Ionian

Dorian - Two Octaves

D Dorian

Phrygian - Two Octaves
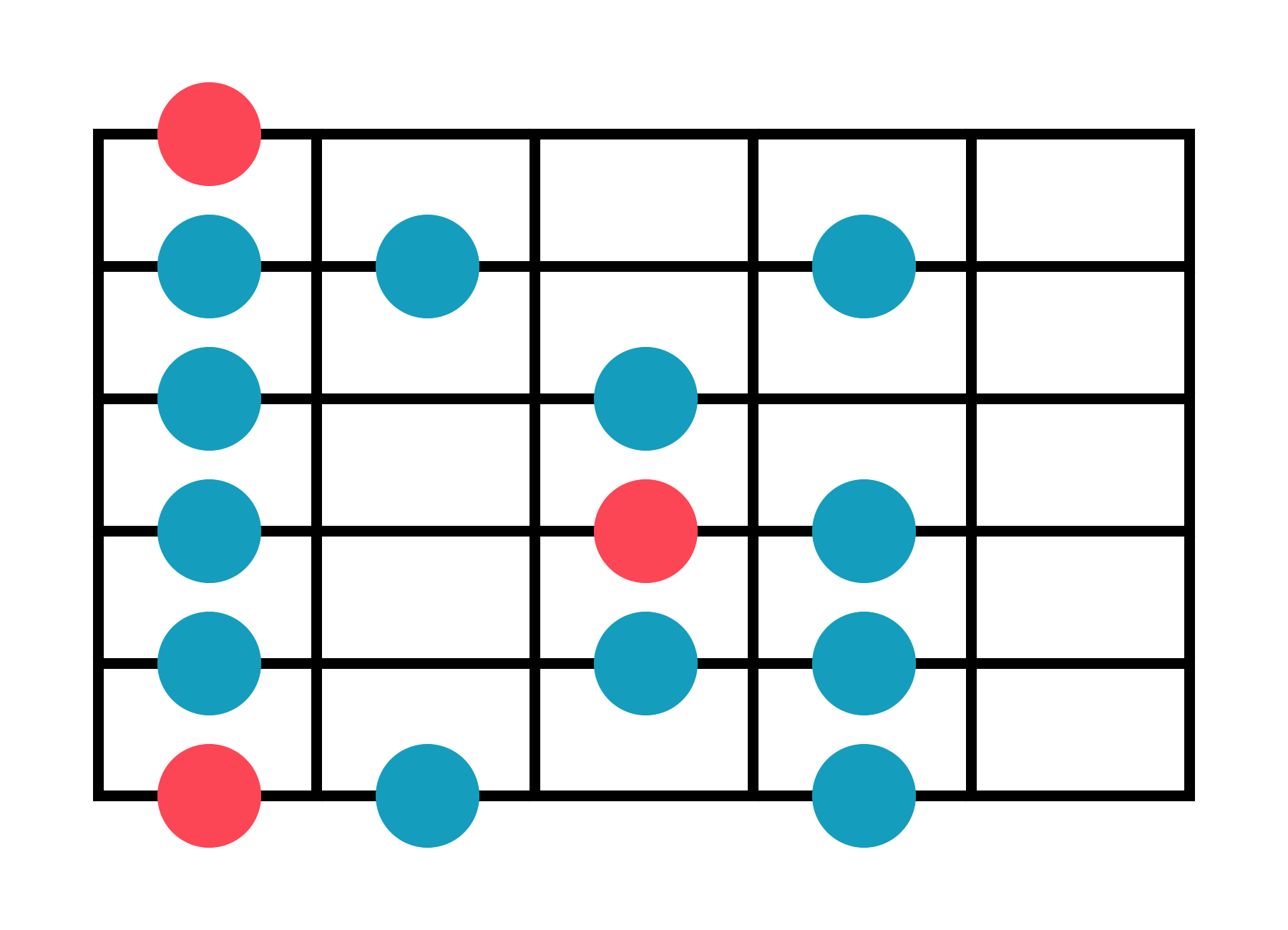
E Phrygian
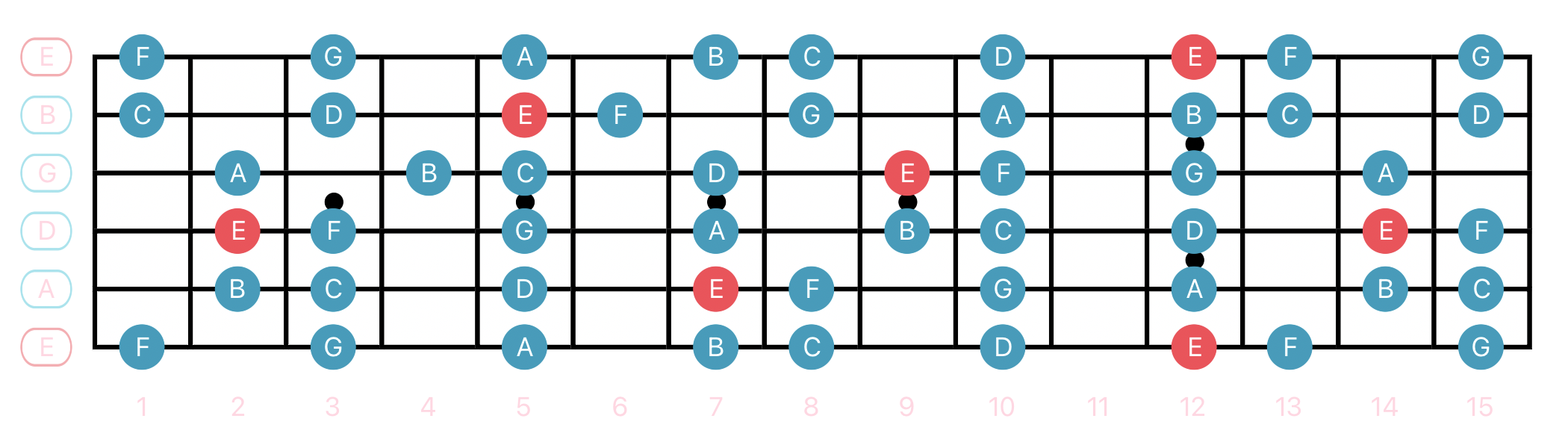
Lydian - Two Octaves
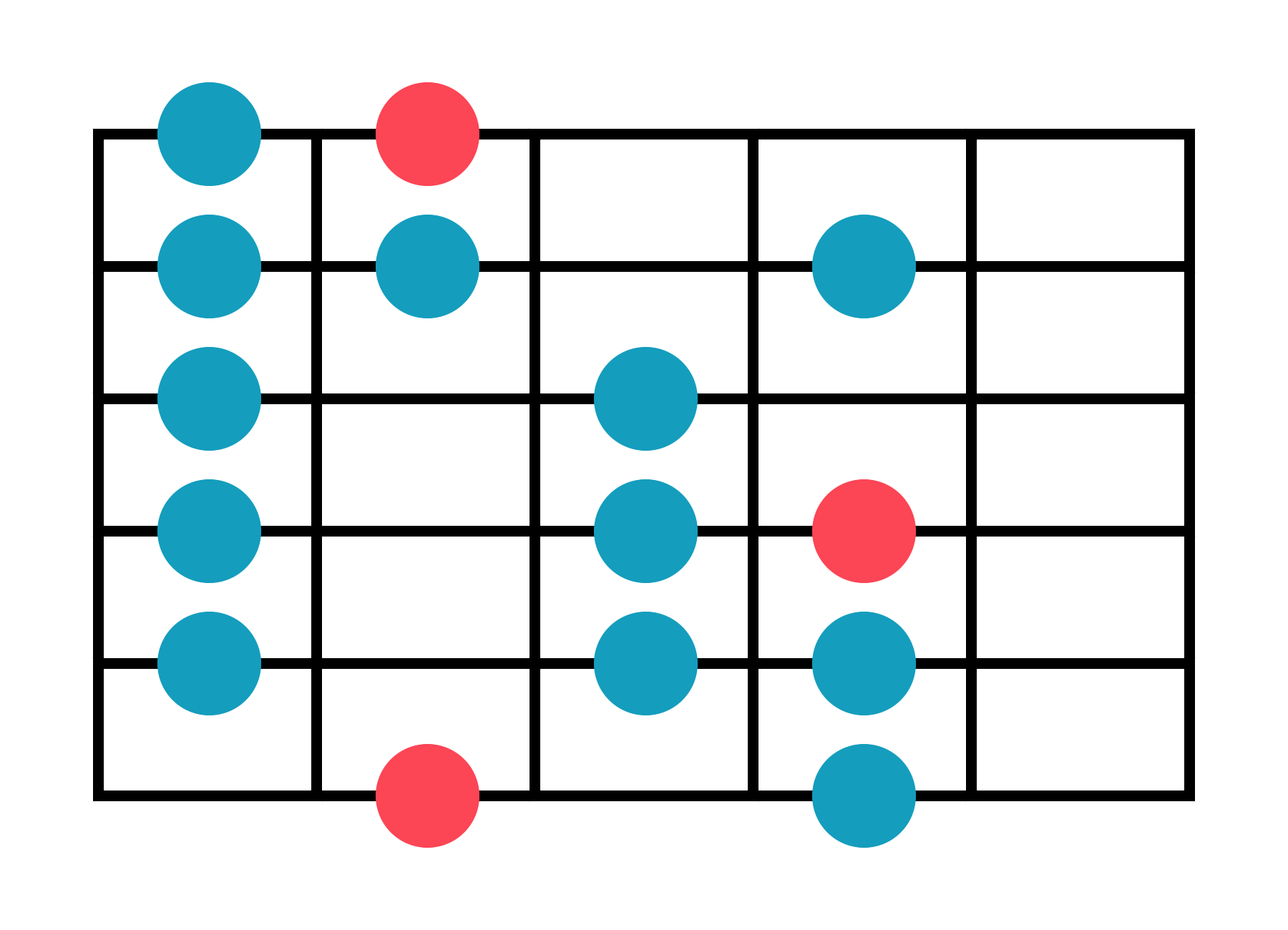
F Lydian
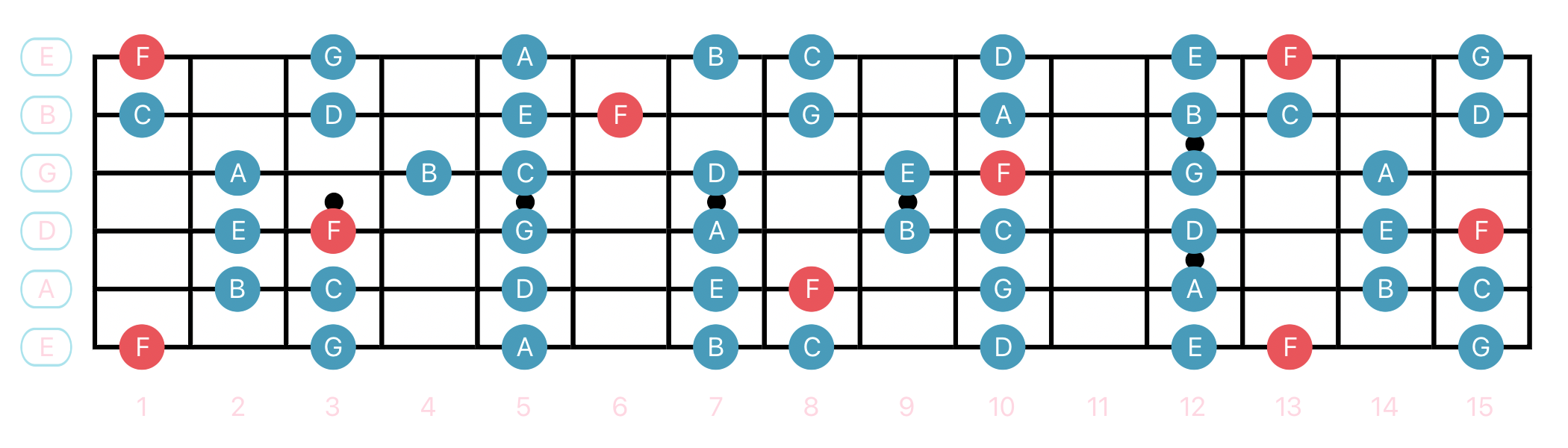
Mixolydian - Two Octaves
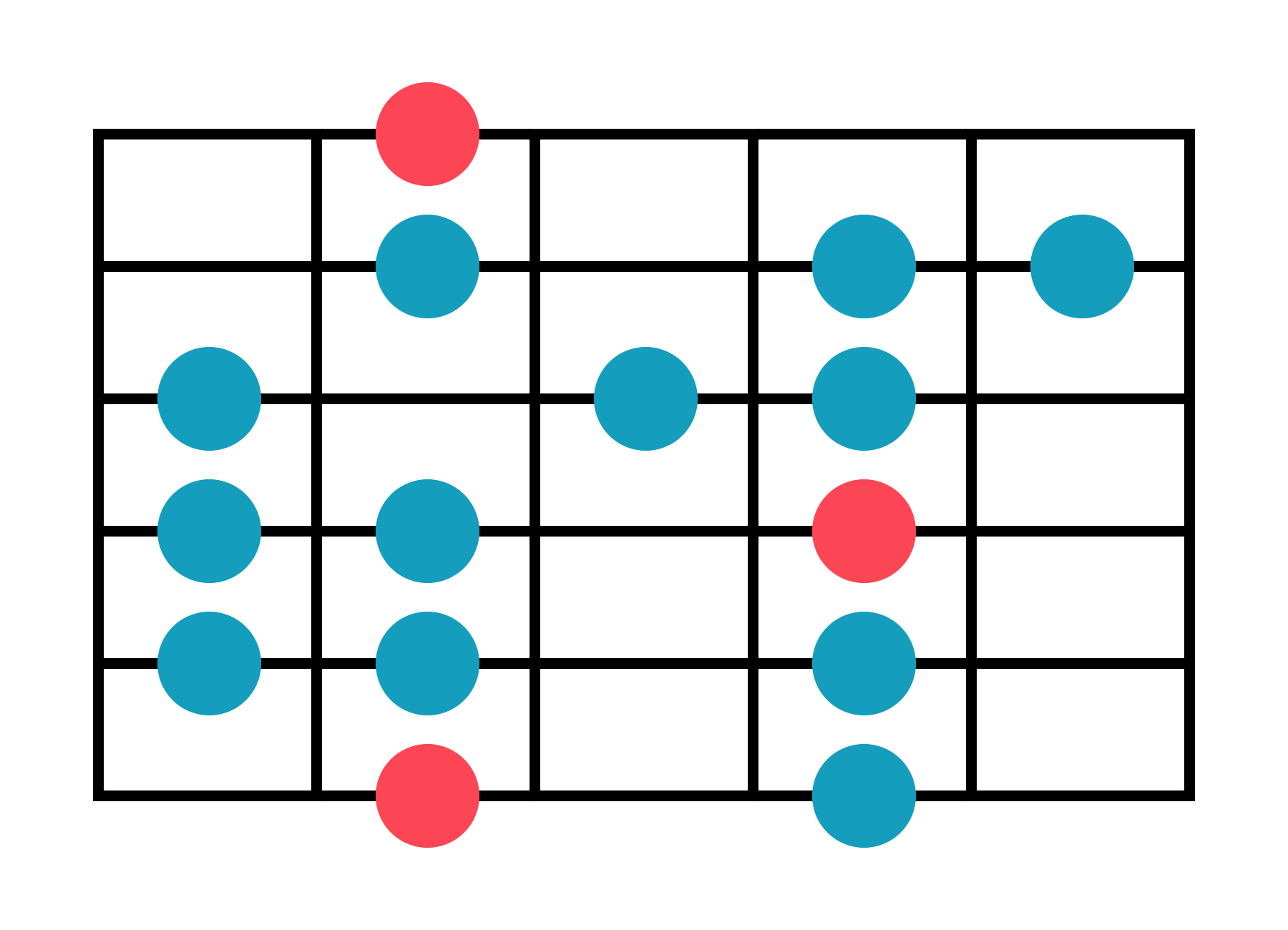
G Mixolydian
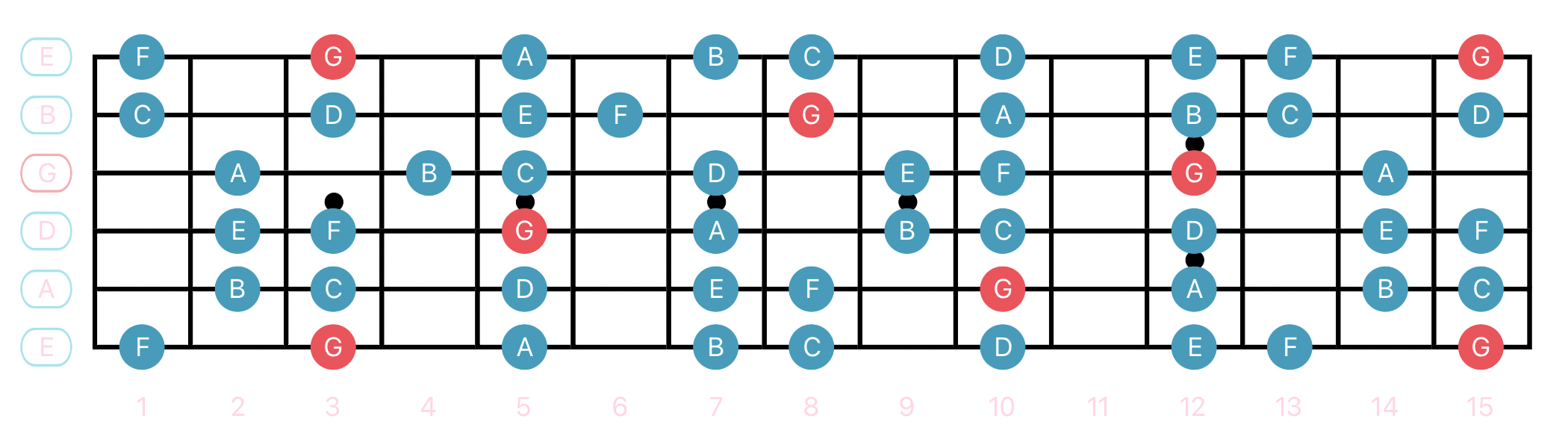
Aeolian - Two Octaves
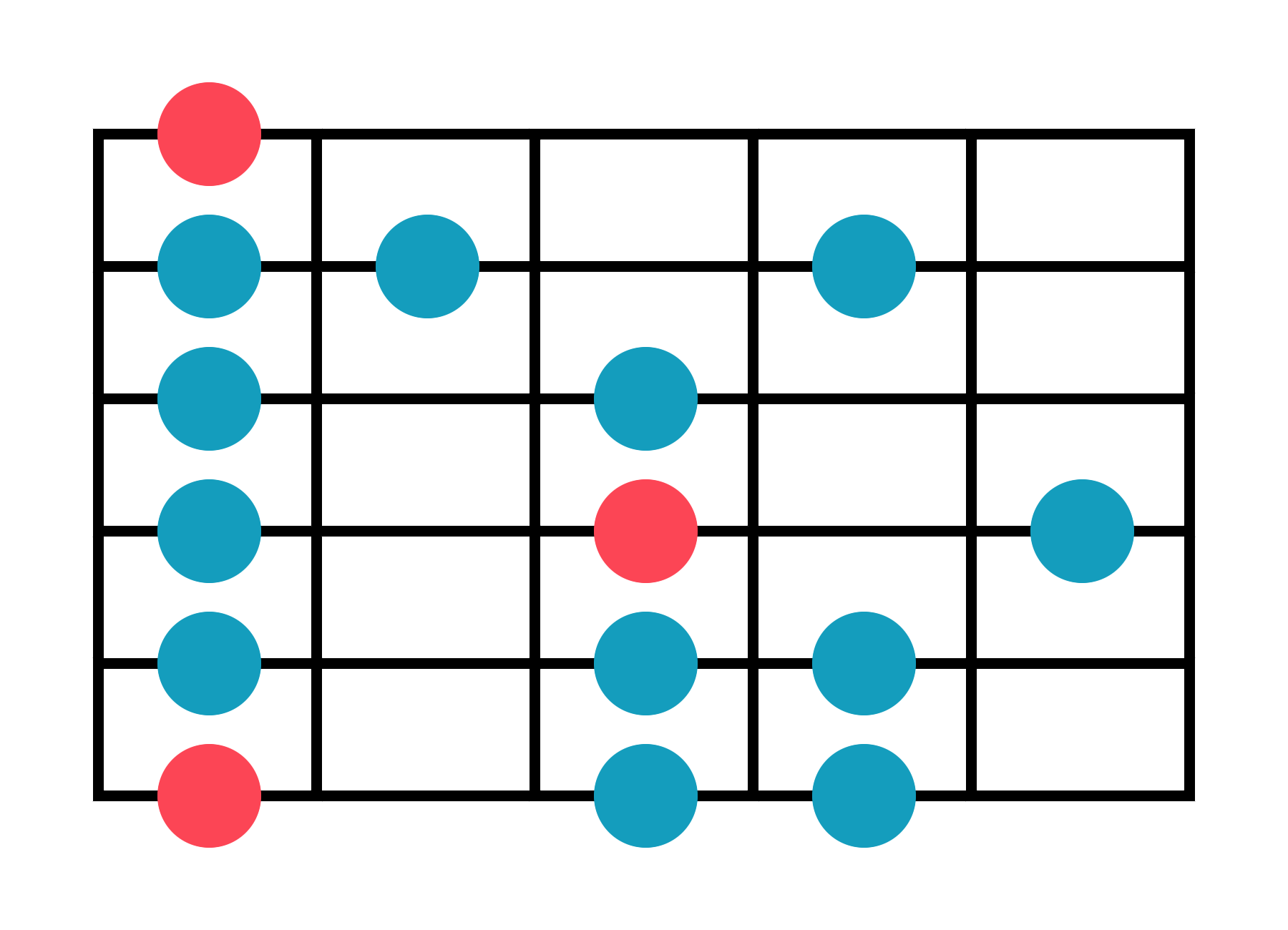
A Aeolian

Locrian - Two Octaves
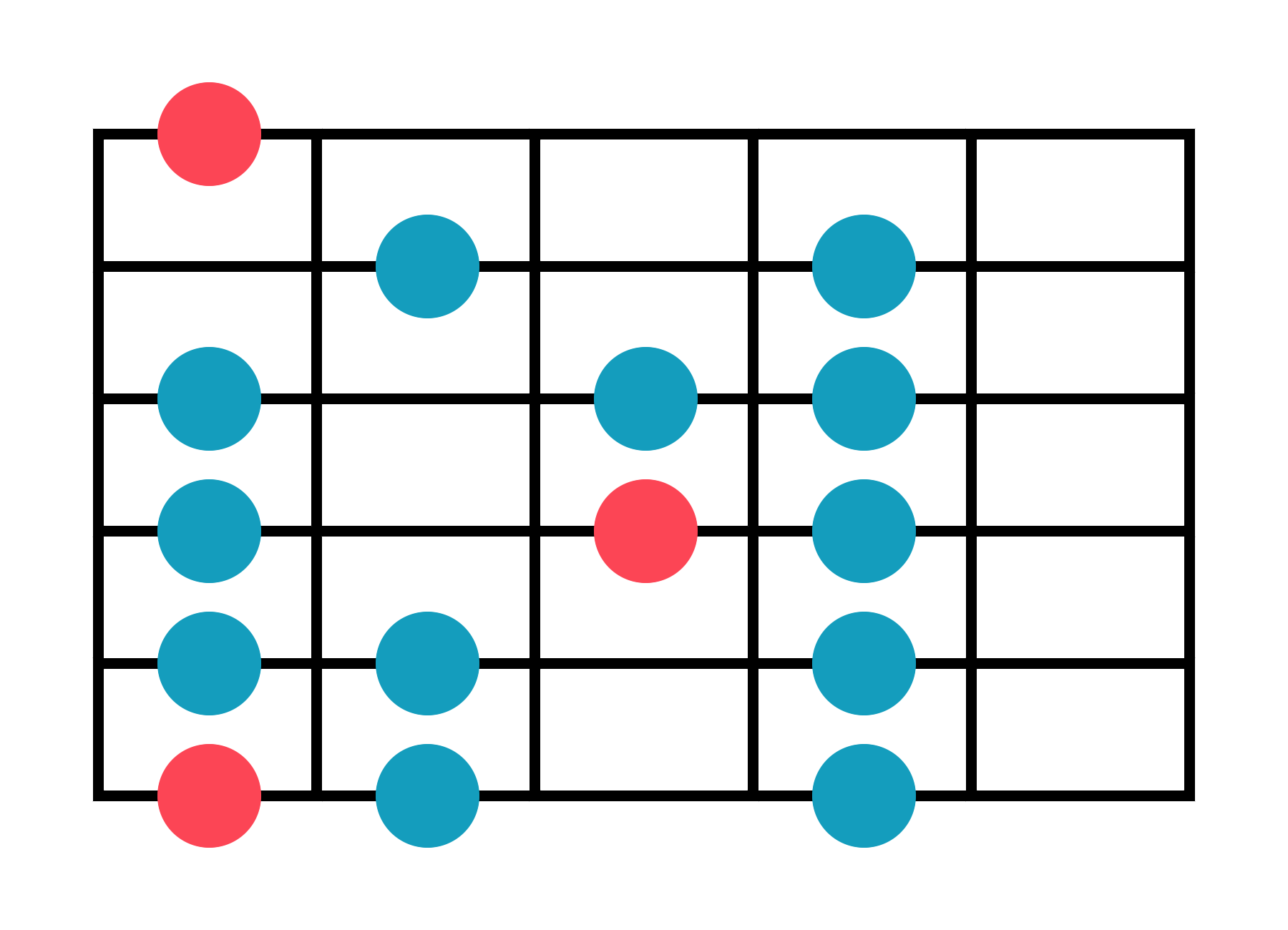
B Locrian
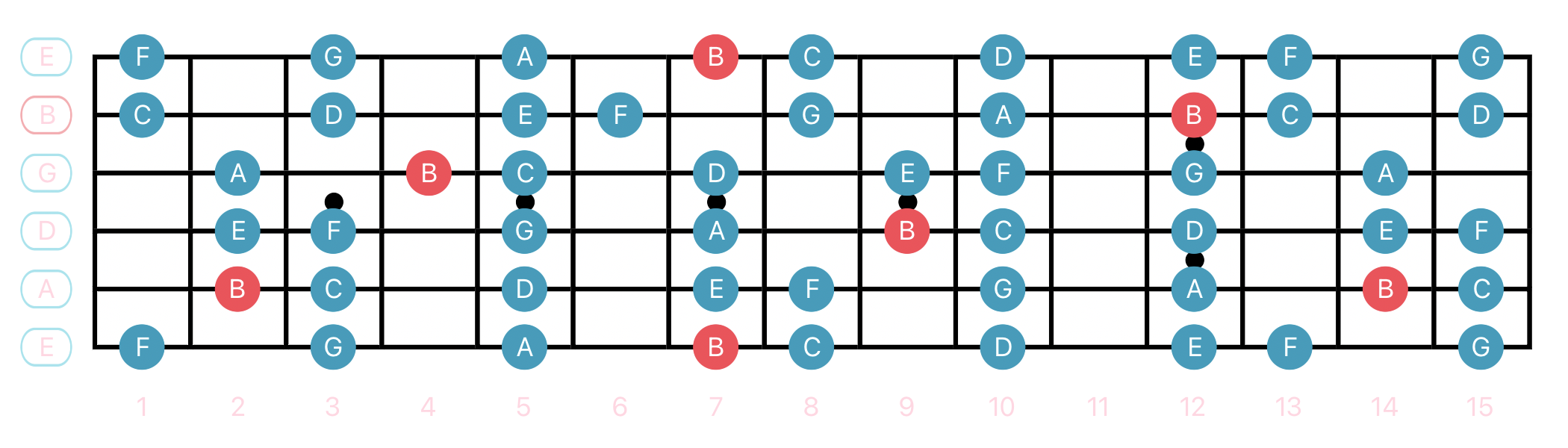
Major Scale - Guitar Modes
Scales in C (parallel)
C Ionian

C Dorian
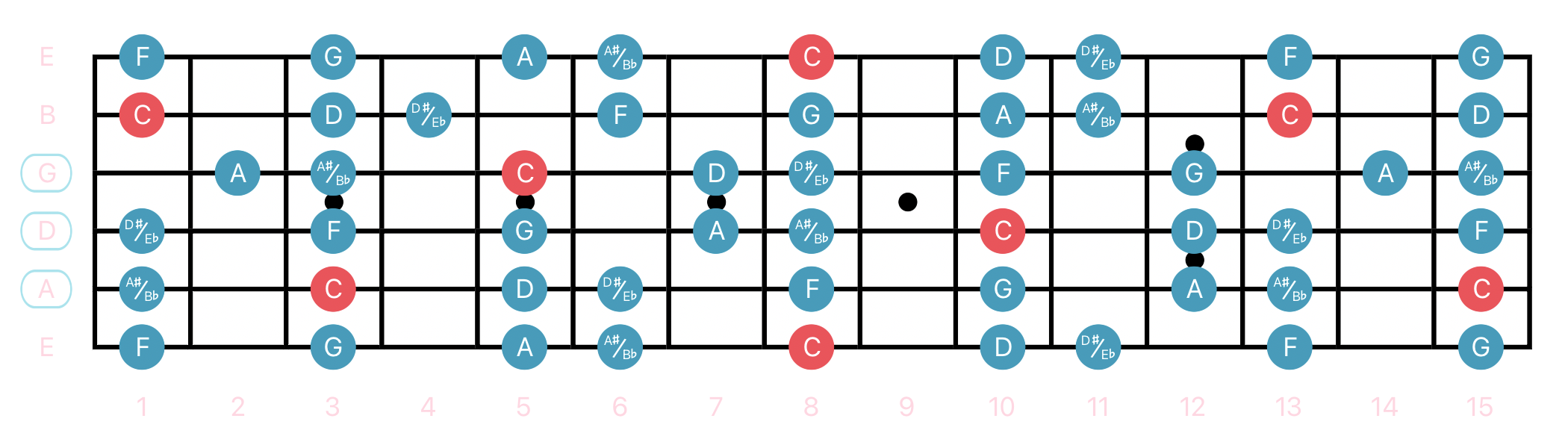
C Phrygian
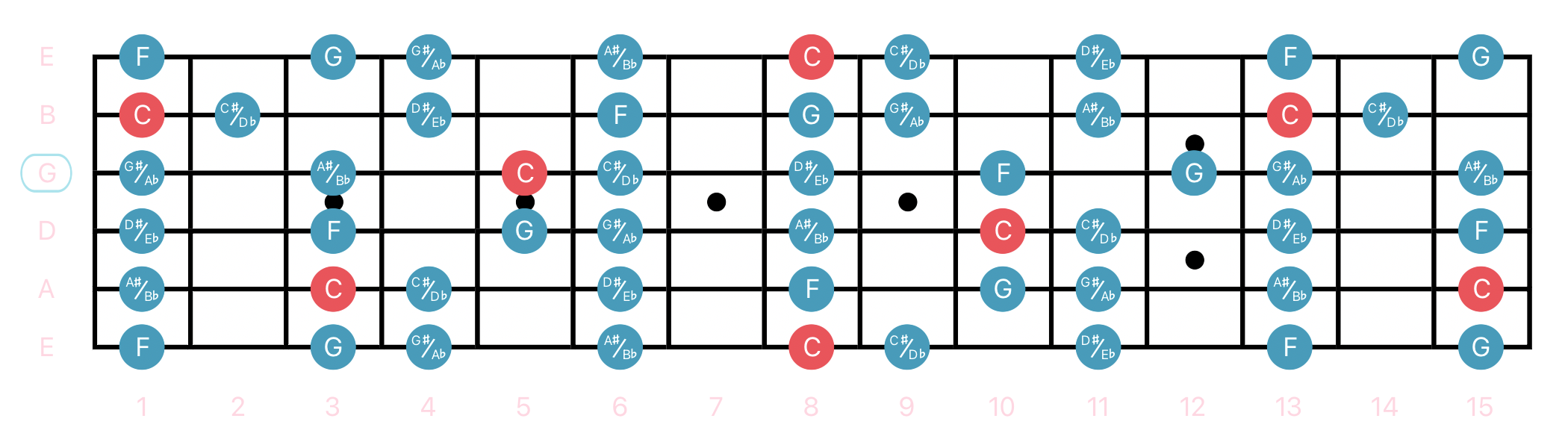
C Lydian
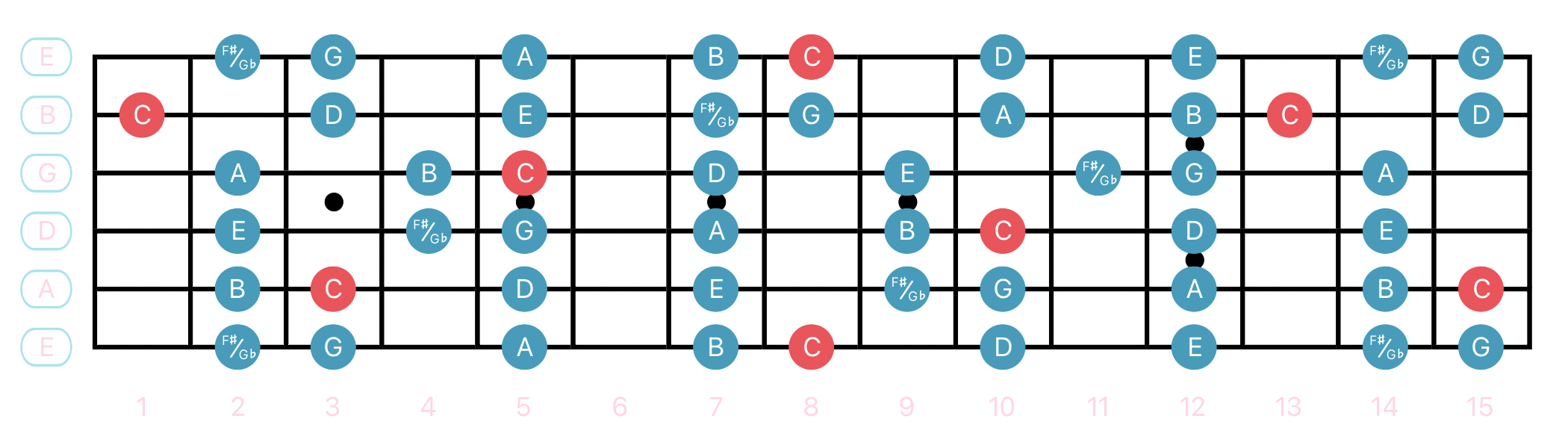
C Mixolydian
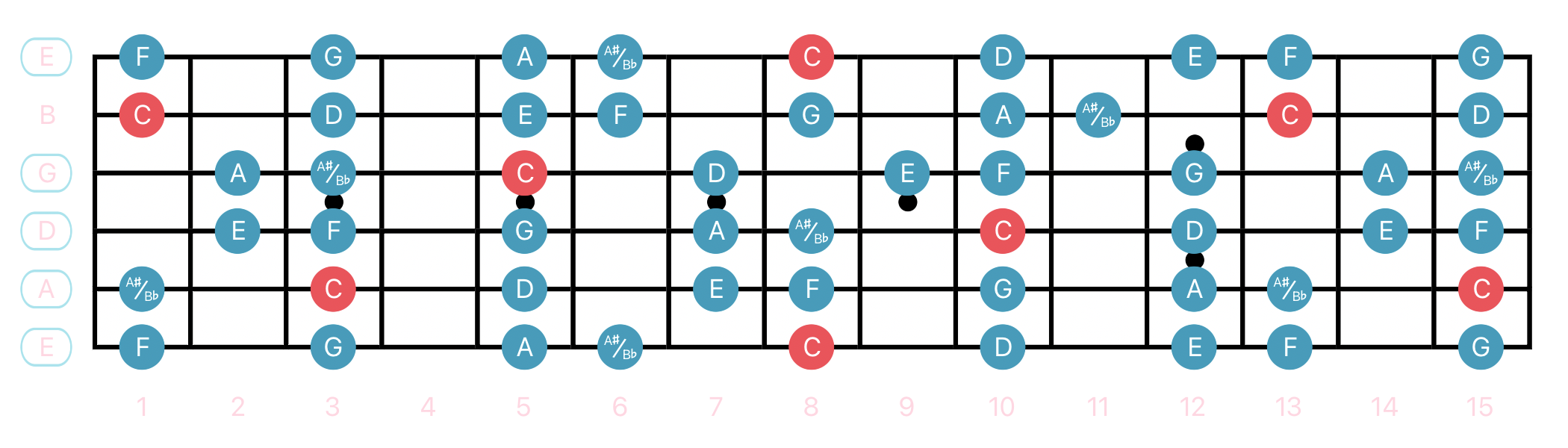
C Aeolian

C Locrian
Published on: December 20, 2023
Edited on: January 14, 2024
